メインコンテンツまでスキップ

解釈可能性 & 説明可能性

AI・機械学習モデルを利用する際の課題​

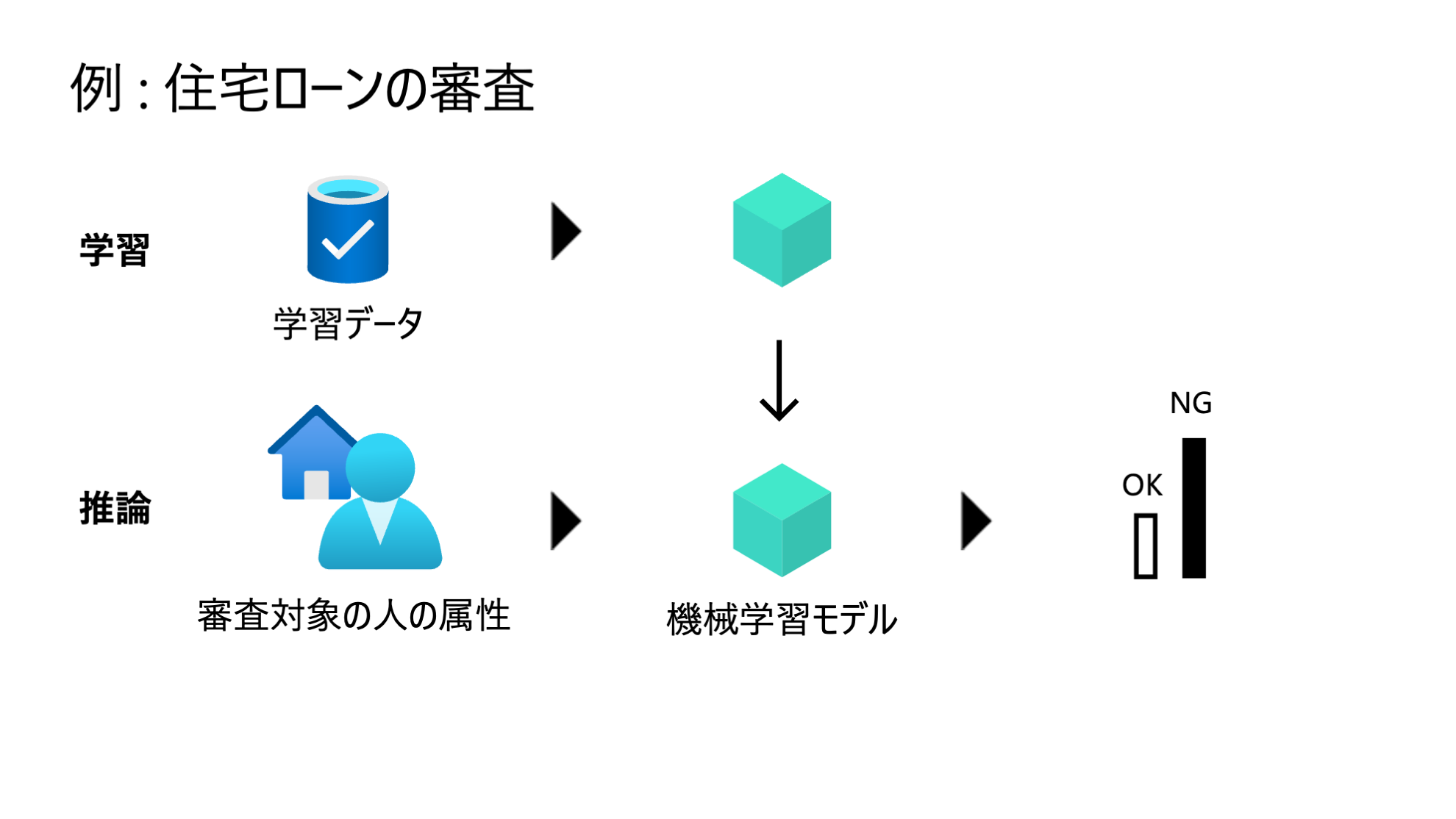
住宅ローンの審査で機械学習モデルが利用されるシーンを考えてみます。上段ではモデル学習が行われ、学習済みモデルが構築されています。下段では業務で利用している様子を表しており、住宅ローンの申し込みがあった際に、モデルによって審査結果が出力されています。

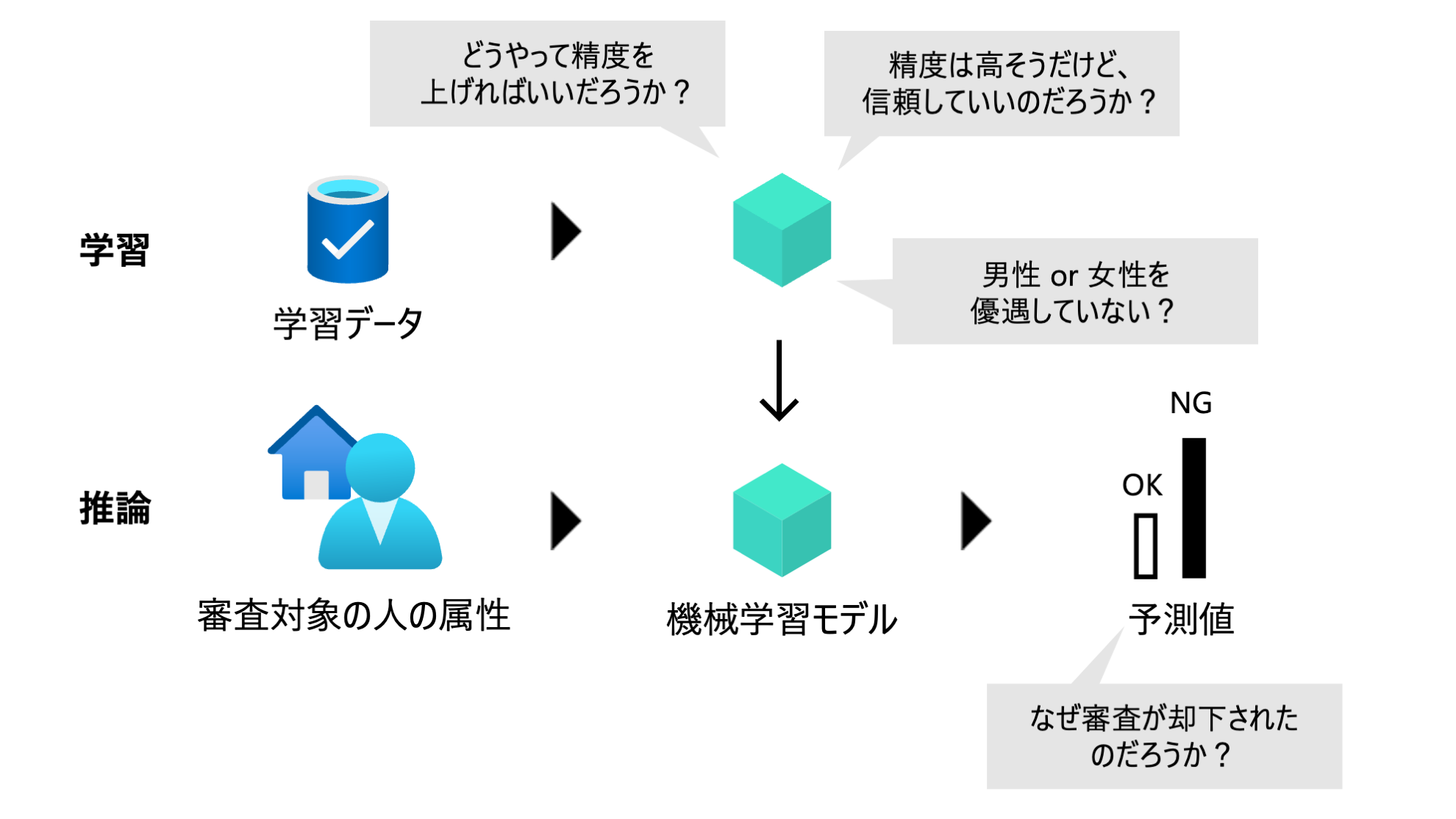
精度がある程度高ければ業務で使えるのか？というとそうではないケースもあります。下図のコメントにあるようにバイアスの問題があったり、予測値に対する説明ができないとなると、ステークホルダーの信頼を失ってしまう可能性があります。

AI・機械学習モデルの社会実装の難しさ​

原因は多岐に渡りますが、AI・機械学習の社会実装の難しさの一つに、AI・機械学習モデルの解釈性・説明性の難しさが挙げられます。例えば、

  • モデルの予測値の根拠が理解できない
  • モデルの品質が不透明
  • モデルの改善方法がわからない

といった点です。そのため機械学習モデルの解釈可能性・説明可能性を高めることが重要になってきます。

人間中心の AI・機械学習のシステム​

システムの関係するさまざまなステークホルダーの視点を考慮して、AI・機械学習のシステムを構築することが重要になってきます。「最先端の機械学習アリゴリズムだからOK」「精度が高いから OK」 とは一概には言えません。

  • データサイエンティスト - 「モデルを改善する方法を知りたい」
  • 事業・製品責任者 - 「ステークホルダーに今後展開するモデルの説明をしたい」
  • ユーザー・顧客 - 「その予測値の根拠を知りたい」

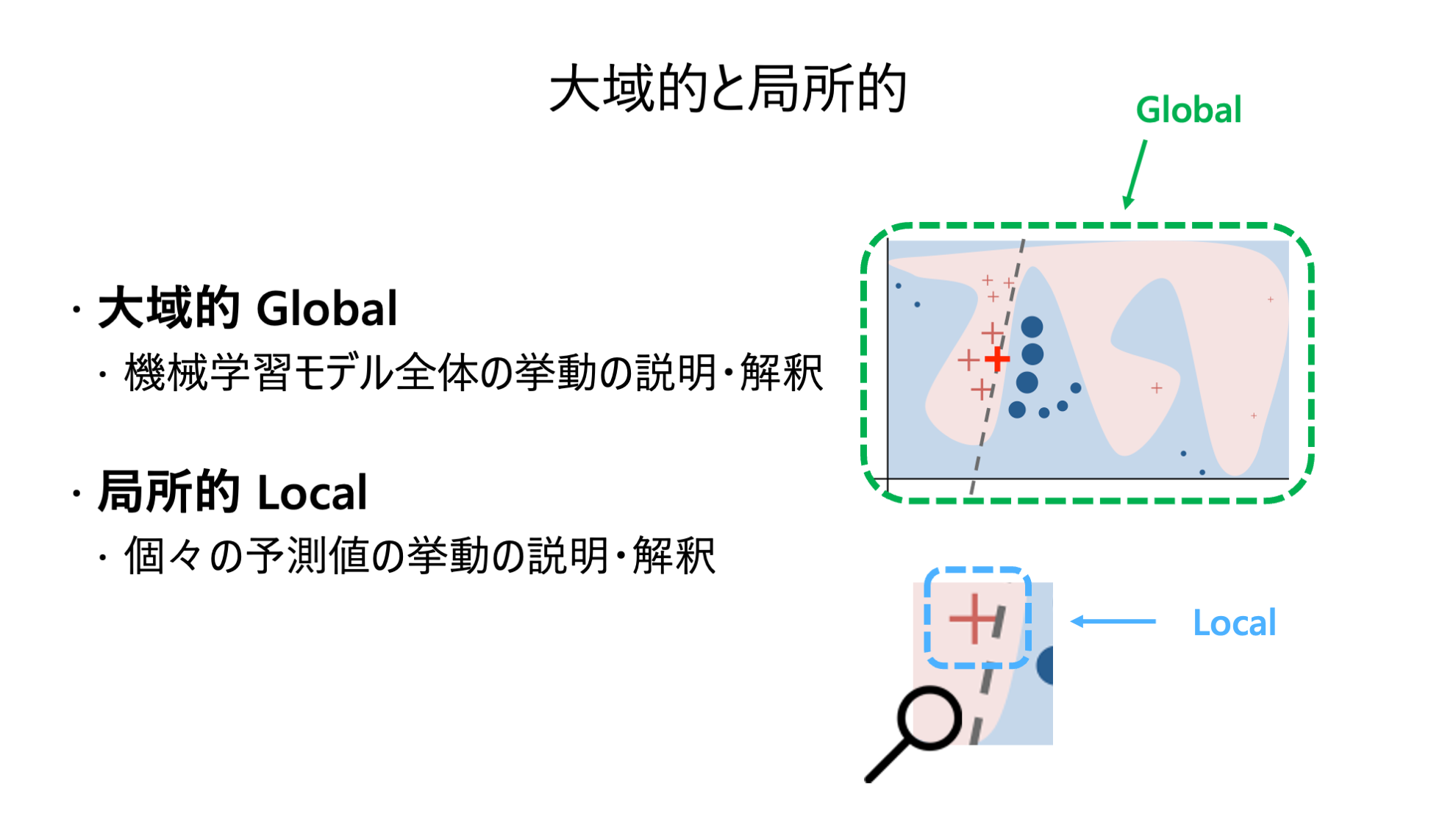
大局的と局所的​

解釈可能性・説明可能性は大きく分けて 大局的 と 局所的 の 2 つに分類されます。

ユースケース​

機械学習モデルの説明可能性と解釈可能性と高めることで次のようなことが可能になってきます。

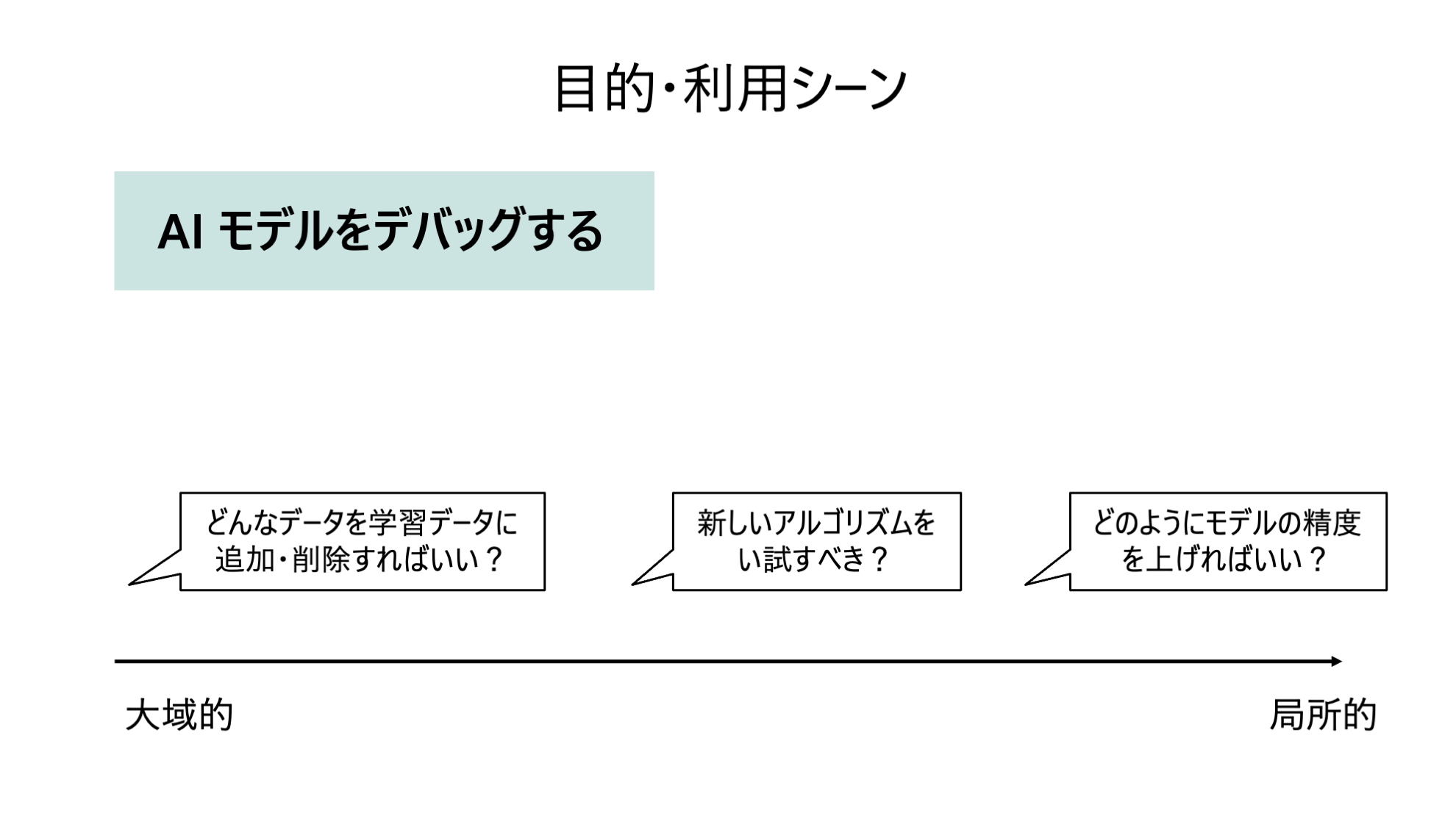
1. 人間の能力を拡張する​

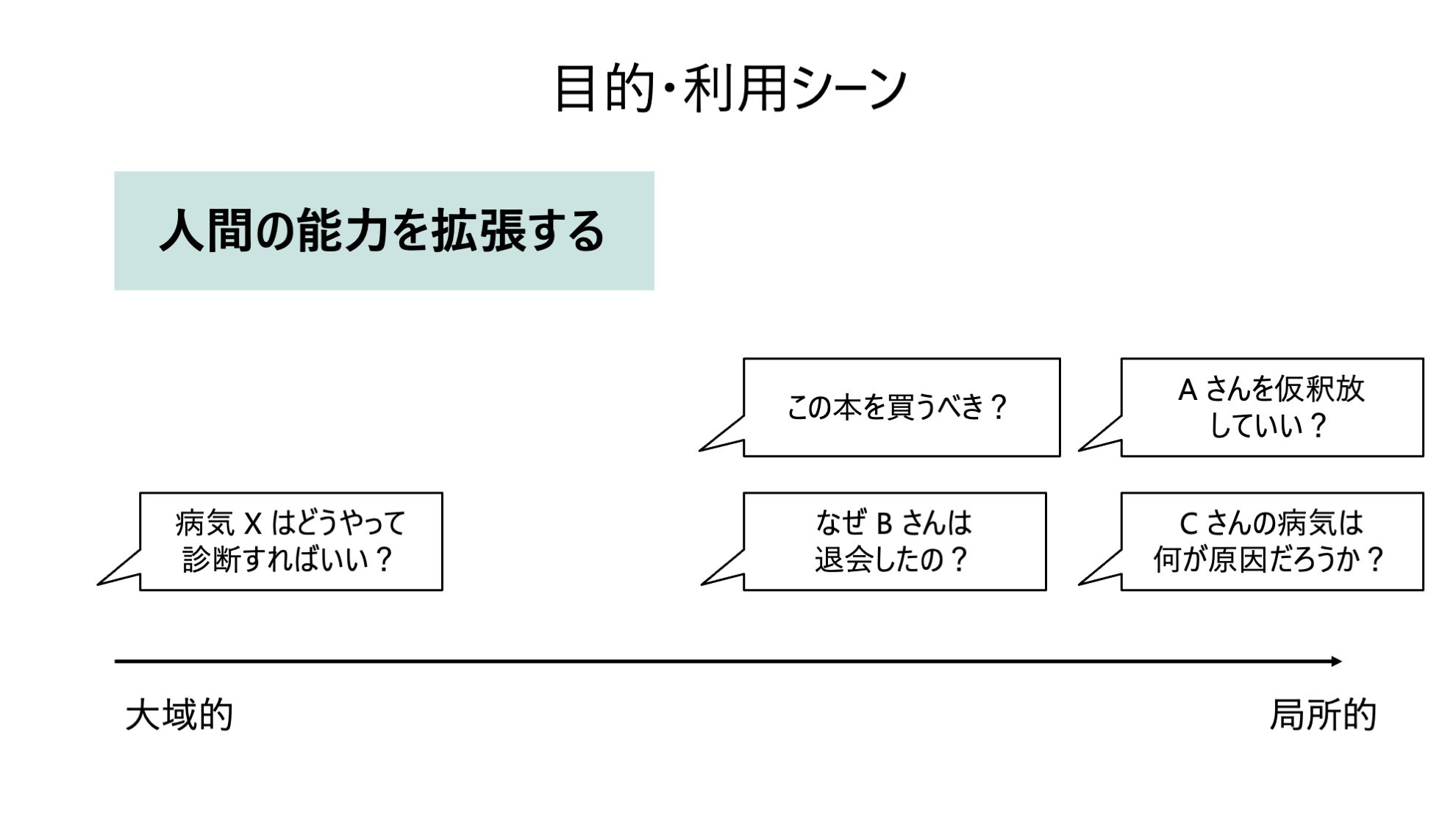
2. AI・機械学習モデルを評価する​

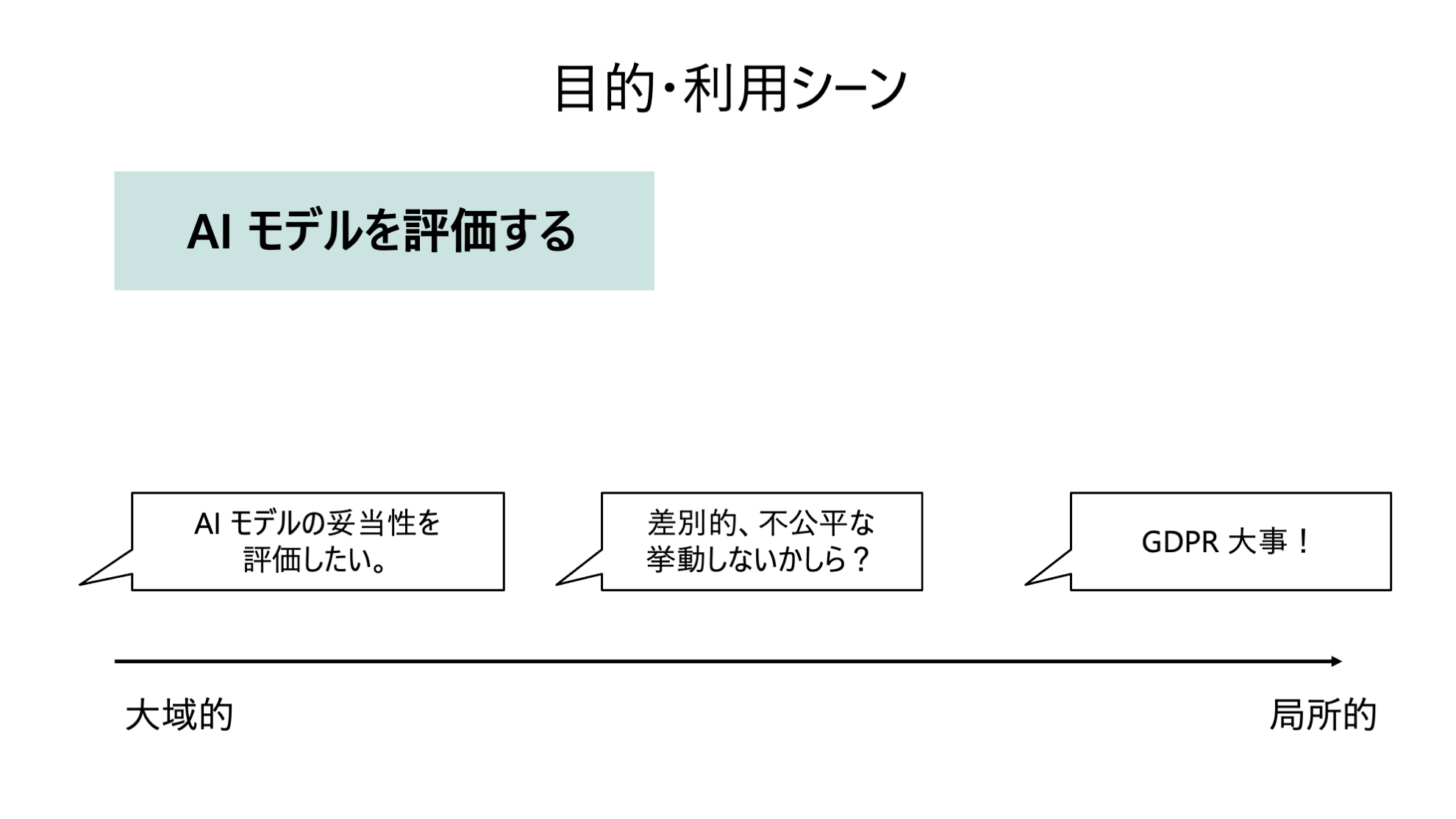
3. AI・機械学習モデルをデバッグする​

解釈可能性 vs 説明可能性​

解釈可能性 と 説明可能性 の違いを見ていきます。

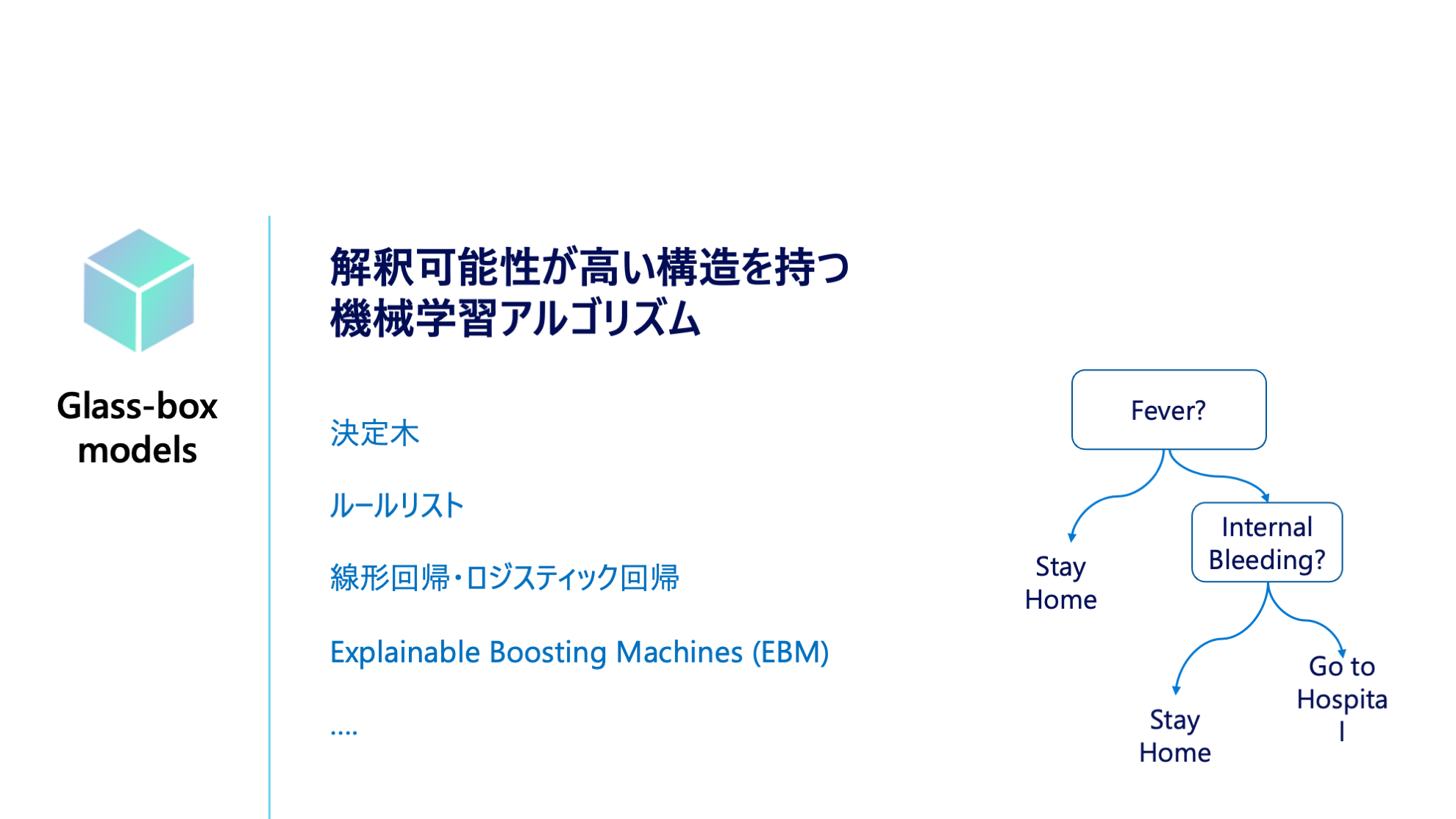
解釈可能性 (Interpretability)​

解釈可能性 の高いモデルとは、機械学習モデルが予測値を算出するまでのアルゴリズム内部の過程が、解釈できる機械学習モデル (Glassbox) を指します。従来の統計的なモデルに加え、最近では一般化加法モデルといった精度が高いながらも解釈可能なモデルが開発されています。


説明可能性 (Explainability)​

説明可能性 が高いとは、機械学習モデルがアウトプットした予測に対して、なぜその予測を出力したのかを説明ことを指します。機械学習モデルを Blackbox として扱います。つまり、内部の構造は考慮せず、機械学習モデルに対する入力と予測値の関係性を見ます。


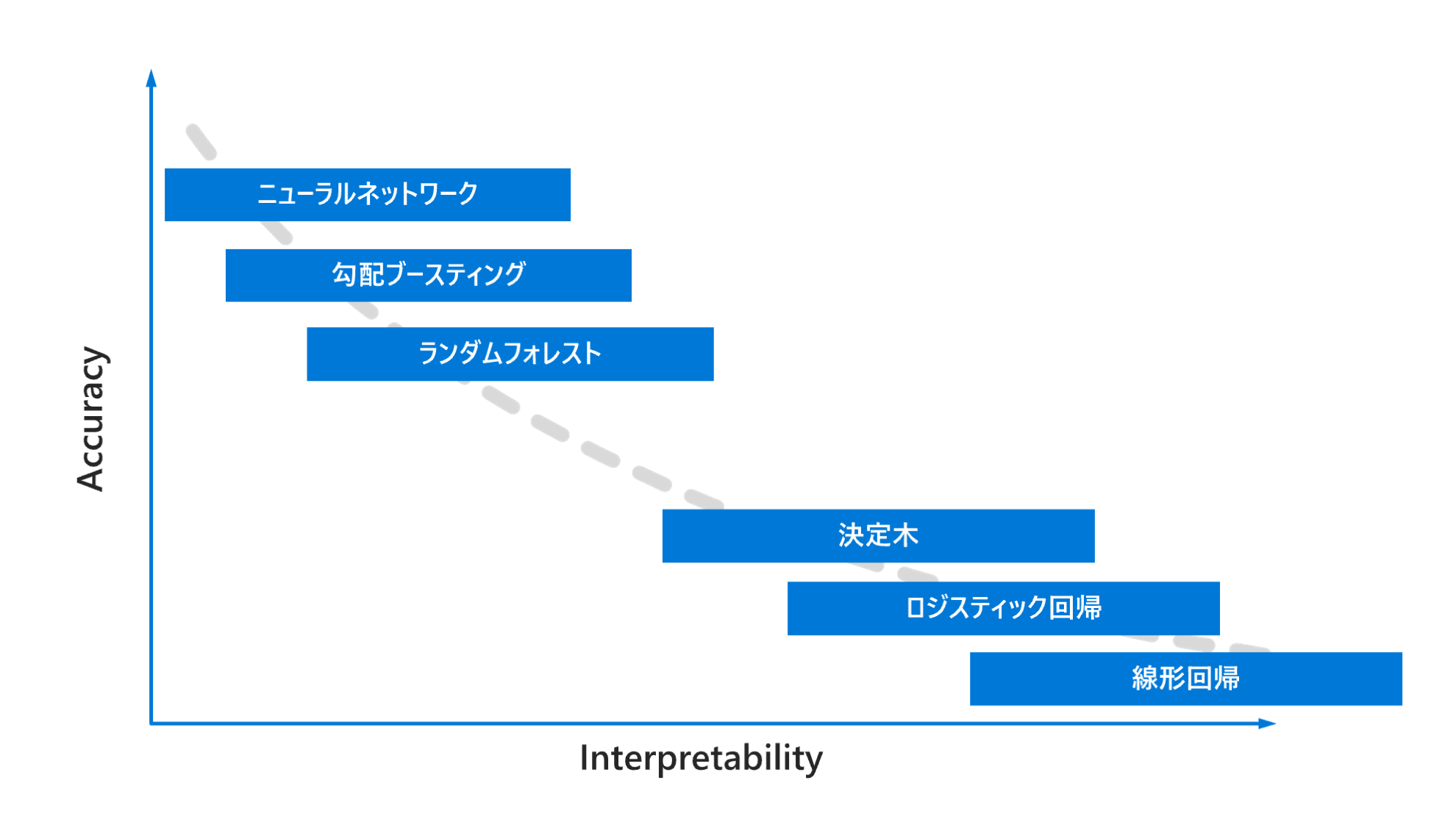
解釈可能性とモデル精度のトレードオフ​

下記の図にあるように一般的には機械学習モデルの精度 (Accuracy) と解釈可能性 (Interpretability) にはトレードオフがあります。精度が高いニューラルネットワークのモデルが開発できたとしても、高い透明性が求められるようなビジネス要件の観点から採用されないことがあります。


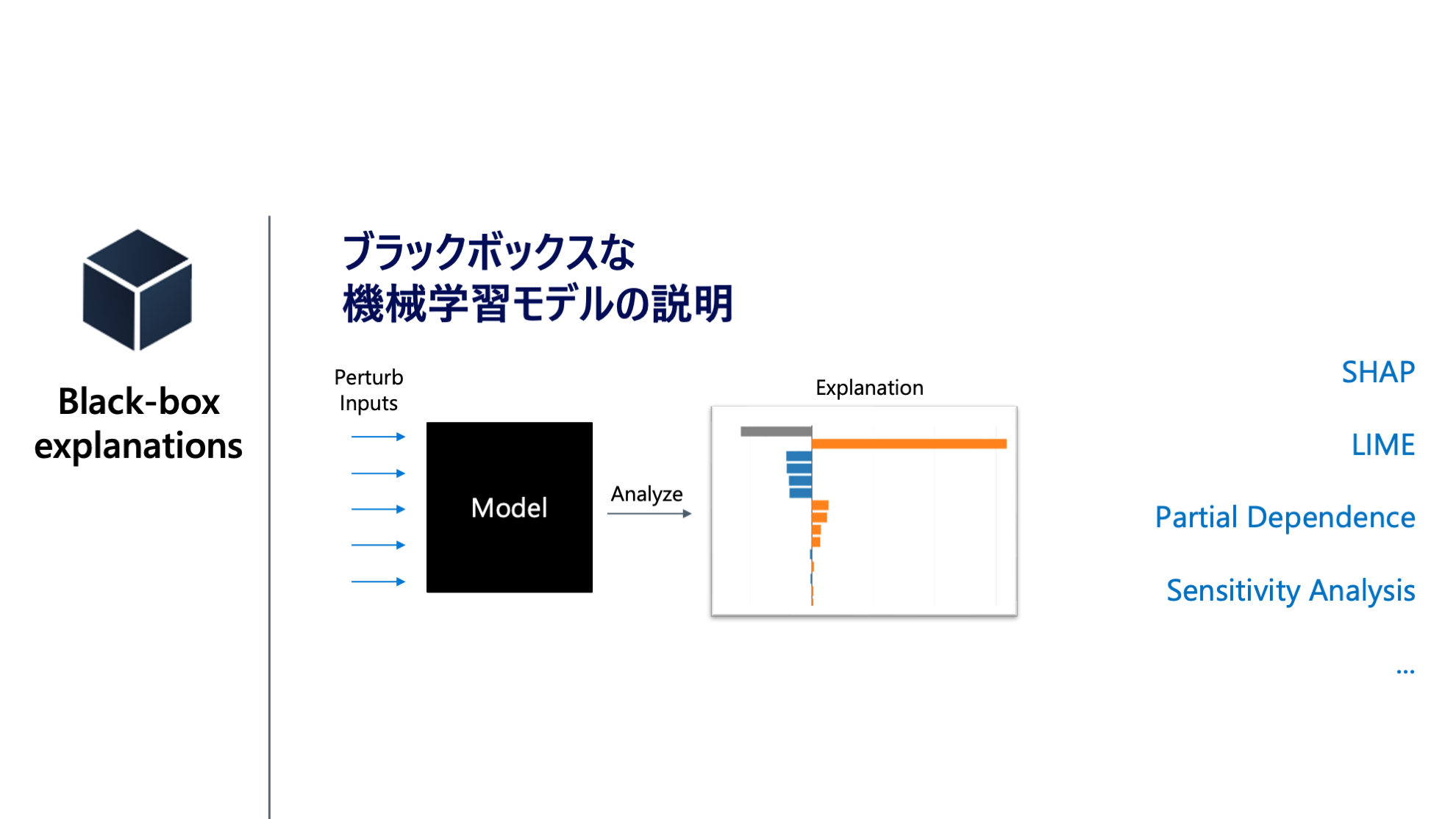
主要なアルゴリズム​

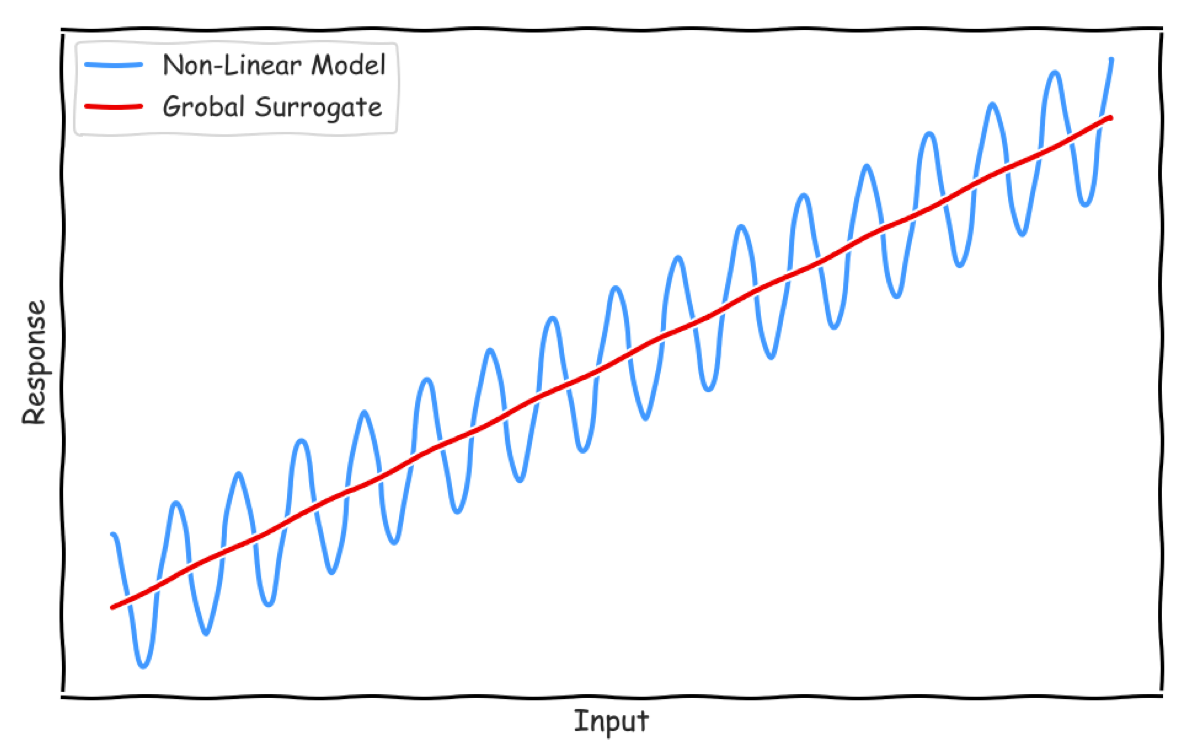
Global Surrogate​

グローバルなモデル解釈方法です。ニューラルネットワークのような複雑な学習済みモデルへの入力データとその予測値を利用し、線形回帰などの解釈可能なモデルを構築します。そのモデルを解釈する手法が Global Surrogate です。InterpretML では LightGBM や線形回帰のモデルが利用できます。



SHAP​

SHAP (SHapley Additive exPlanations) はゲーム理論のシャープレイ値の枠組みを利用して、モデルの種類に関わらず、ここのデータの特徴量ごとの貢献度をみることができます。SHAP 単体でもライブラリが公開されています。


※ Trust and understanding of AI Models’ predictions through Customer Insights より引用


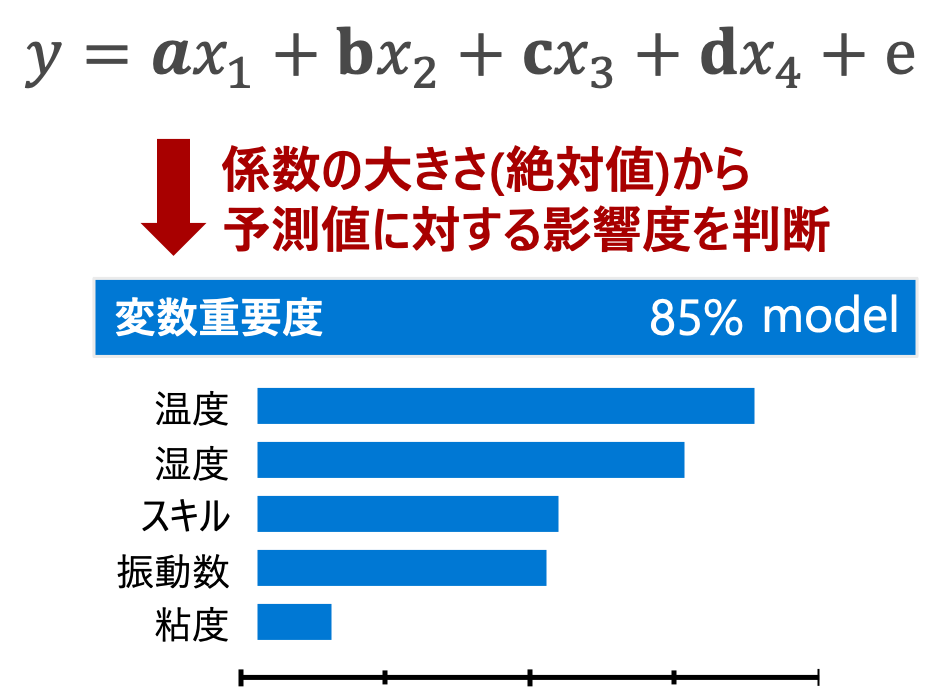
線形回帰モデル​

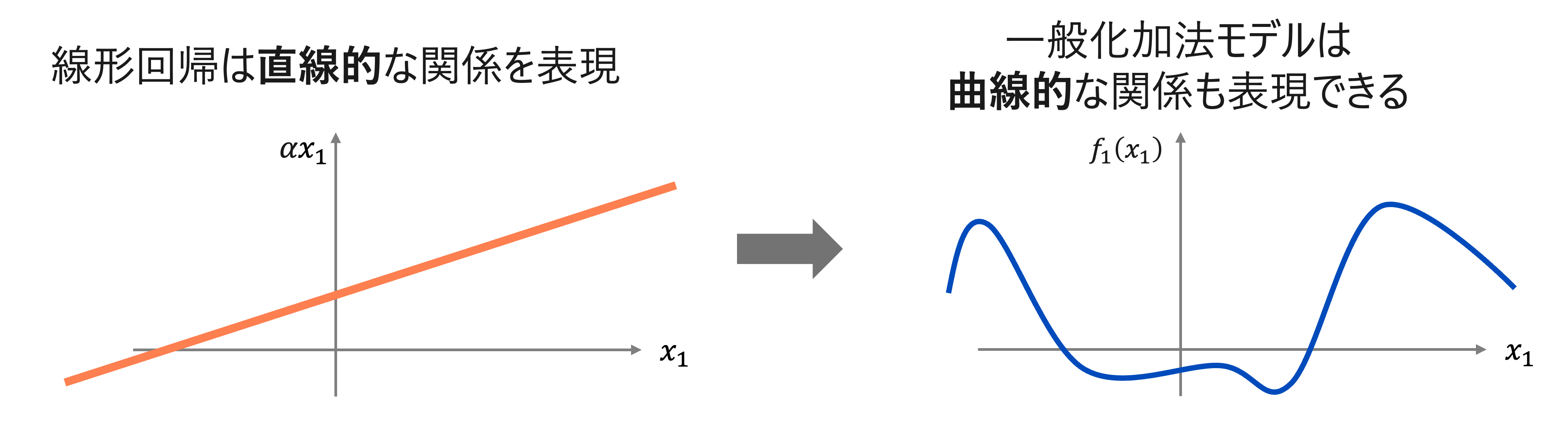
線形回帰モデル は、各説明変数の値に重みをかけたものを合計する線形的な関係を表現します。

Y=αx1+βx2+γx3+...+ϵY = \alpha x_1 + \beta x_2 + \gamma x_3 + ... + \epsilon

通常、各変数の重みの大きさを変数の重要度とし、予測値への影響を判断します。



決定木​

説明編数をある基準で分割し、分割された各領域における目的変数の値を予測値とするモデルです。分割によってどのくらい目的変数を正確に予測できるようになったのかをみて、変数の重要度を算出します。

これは、工場の製造工程において、不良の確率が 20% のデータに対して決定木モデルを構築した場合のイメージ例です。


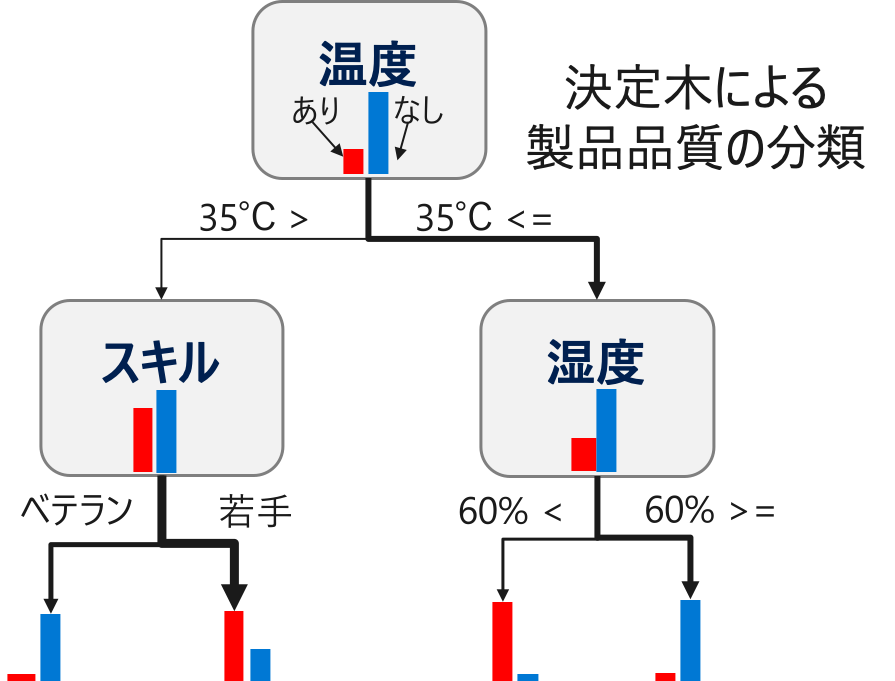
例えば、「温度が35℃以上」&「湿度が60%以上」 であれば不良の割合がかなり多いことがわかります。一方、「温度が35℃以下」&「スキルがベテラン」 の場合は不良の割合が少ないです。

このように決定木は、どういった条件で予測値が算出されるのかが明確なので、解釈性のあるモデルです。


一般化加法モデル​

一般化加法モデル (Generalized Additive Model; GAM) は、各説明変数ごとに非線形関数を学習します。この関数の出力を足し合わせたものが予測値になります。線形回帰などの線形モデルとは違い目的変数 yy との関係性は線形性は前提としていません。

Y=f(x1)+f(x2)+f(x3)+...Y = f(x_1) + f(x_2) + f(x_3) + ...

線形回帰モデルと一般化加法モデルの違いのイメージ



Explainable Boosting Machines (EBM)​

Explainable Boosting Machines (EBM) は、一般化加法モデル (GAM) に交互作用項を組み込んだモデル (GA2M) を高速に推定するアルゴリズムです。

Y=f(x1)+f(x2)+f(x3)+...+Σijfij(xi,xj)Y = f(x_1) + f(x_2) + f(x_3) + ... + \Sigma_{ij} f_{ij}(x_i, x_j)

この関数を推定する方法はいくつかありますが、EBM ではこの関数をブースティングで推定します。また交互作用項を推定するアルゴリズム (FAST) も実装されており精度向上に寄与しています。

参考情報​